by Dr. Boris Zakharov
ABOUT THE AUTHORS

Dr. Boris Zakharov
Professor Boris Zakharov began his professional career in the “Kedrovaya Pad Natural Reserve” (Far East State University, Vladivostok, Russia) as a research scientist, where he participated in and performed various scientific projects in field zoology. For five years, from 1974 to 1979, he collected invertebrates, processed zoological materials and monitored seasonal and long-term dynamics of natural ecosystems. For several years after that, Dr. Zakharov worked in the Institute of Agricultural Chemistry (Novosibirsk, Russia), where he received intensive and in-depth experience in the study of pest control and modern methods of crop protection. Dr. Zakharov's Doctoral research was on horse flies (Diptera, Tabanidae), beginning in 1983 at Novosibirsk Biological Institute. The results of this study were published in his papers and concern systematics, ecology, biogeography and cattle protection from blood sucking diptera in Siberia.
After his arrival in the United States, Dr. Zakharov participated in a project on ground spiders of Australia and New Zealand in the American Museum of Natural History, where he has worked from 1996 to 2005 as a Curatorial Assistant in the Spider laboratory in a Department of Invertebrate Zoology. Currently, he occupies the position of a visiting scientist at the American Museum of Natural History, where he continues the study of ground spiders of the world.
Professor Boris Zakharov began to teach in 2005 at Hostos Community College/CUNY. Boris joined the Natural Sciences department at LaGuardia in 2009.
Before we can talk about the Life in the Universe, we have to identify what Life is to know what we are actually looking for. As it always happens with the most “simple” fundamental definitions (like, for example, with the definition of a dot in geometry or matter in physics), to get an unambiguous simple definition is not so easy, if possible at all. And there are many different definitions that emphasize one or another properties of living organisms. However, all known living organisms are characterized by a stable (for comparatively long time) set of chemical reactions organized into sequences or metabolic pathways. Thus, any process that leads to the emergence of structures characterized by stable metabolic pathways is a prerequisite to the existence of Life.
Chemical reactions can be classified into many classes, but, ultimately, all of them are characterized by a transfer of atoms and/or energy. According Thermodynamics, if somewhere in Universe there are physical environments that permit the existence of some diversity of chemical elements (first of all H, O, C, N, P, and S) unequally distributed in space, there always exists such a transfer of energy and matter. In a closed system this transfer ends very fast with equilibrium, but in an open or partially-open/closed system, the transfer may exist indefinitely and even increase.
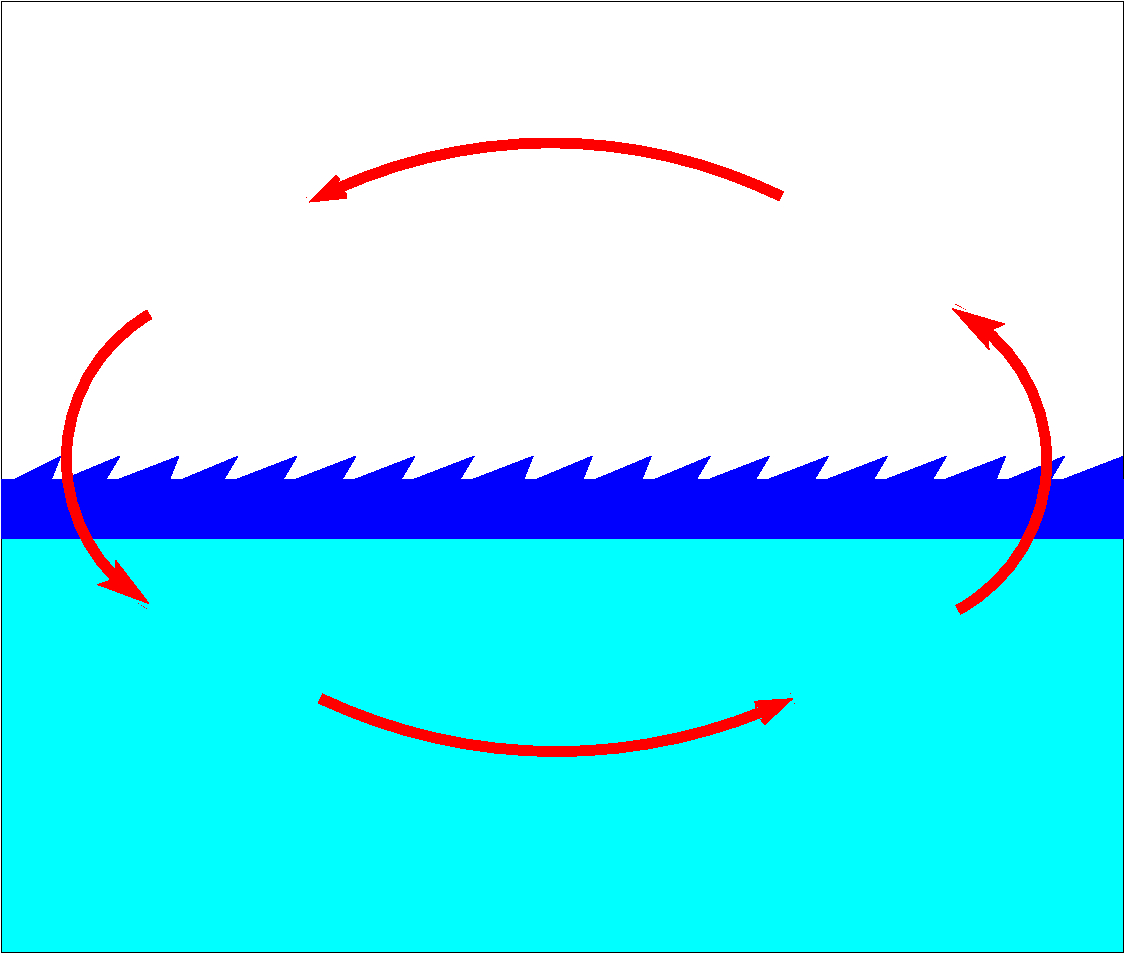
Figure 1. Circuit of matter and energy between two media.
Let's imagine a lifeless planet where there are at least two media: liquid (water) and gas, and varying temperature. Our knowledge suggests that in this planet inevitably develops currents of chemical elements and energy that will tend to organize into stable circuits (Fig. 1). Such kind of circuits will develop everywhere where there exists an unequal distribution of matter and energy: between solid and liquid medias, solid and gas, and even between two solid media, as it is observed in the Earth crust with its continuous migration of heavy chemical elements towards the center and light chemical elements towards the Earth surface.
Simple chemical reactions follow the principle of LeChatelier, which is a specific application of physical conservation law. According this principle chemical reaction between two reactants tends to reach an equilibrium and may go in both directions:
\[ {A+B \rightleftharpoons C+D }\]
Metabolic pathway contains sequence of dozen or more chemical reactions:
\[ \underrightarrow{ { A+B \rightleftharpoons C+D \rightleftharpoons E+F \rightleftharpoons G+H \rightleftharpoons \cdots} }\]
Every single reaction in this chain follows LeChatelier's principle, but organized into the chain they become less and less reversible, i.e. the total result of these reactions is a directed process. This example demonstrates how increase of complexity of the process leads to increase of its stability. The accidental development of chemical bonds and creation of molecules results in emergence of robust stable metabolic pathways with less space for accidents.
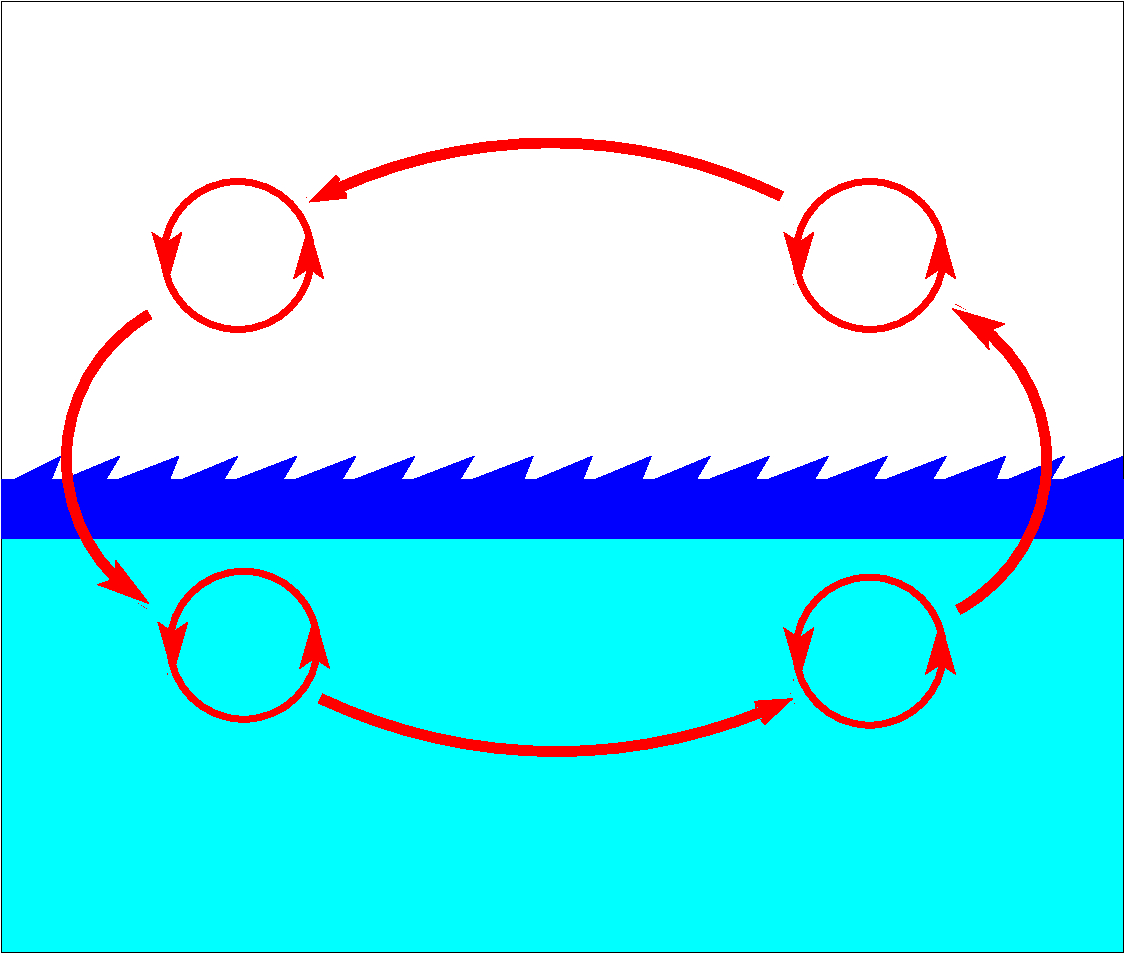
Figure 2. Fracturing of global circuit on.
Fracturing one single metabolic pathway into smaller circles increases total robustness of matter and energy circulation (Fig. 2). The emergence of lipids and, particularly, phospholipids, results in development of membranes and bubbles that separate media into small compartments and increase heterogeneity of the whole system. A phospholipid molecule is characterized by having two sides. One side of the molecule has negative electric charge, whereas another side of the molecule is neutral, i.e. has no electric charge. The electrically charged part of the molecule creates weak hydrogen bonds with electrically charged water molecules. The neutral side of the phospholipid molecule stays away from water and does not mix with it. Mixture of phospholipid molecules with water always results in their self-organization in a phospholipid bilayer, where hydrophilic sides always turn toward water molecules, but hydrophobic sides hide inside a bilayer. Ability to create the same structures every time when there are appropriate circumstances is called self-organization. Self-organization is among the most fundamental properties of Life.
The modern dominant paradigm of individual development states that this process is programmed by the genome, where a switchover in gene network (regulation of gene expression) is determined by a positional information. But what is positional information? How is the integral space-time pattern of positional information generated? The emergence of complex organisms from eggs or buds cannot be explained in terms of a genetic program for the very simple reason: generation of a three-dimensional macroscopic form cannot be explained in terms of molecular composition. Composition does not determine form. Organism development cannot be governed by the autonomous enrolling of genomic information. On the other hand, the process of gene expression has to be under control of some “global factor,” which governs the whole process and determines organism's unity as a system.
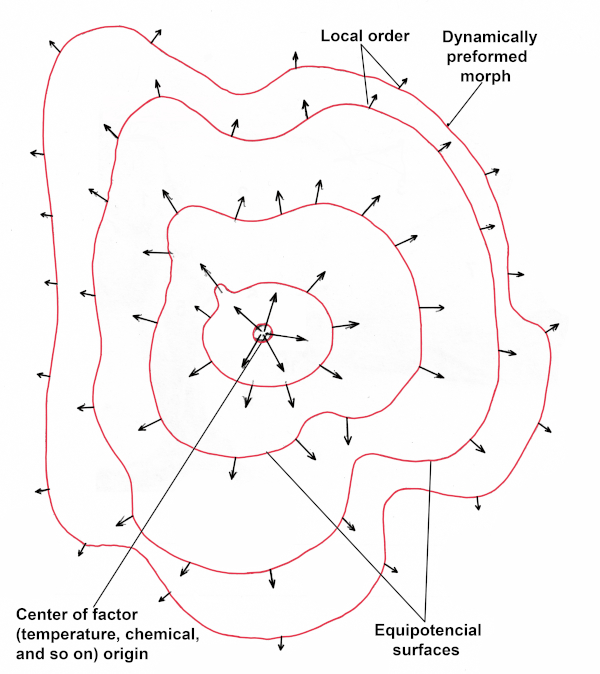
Figure 3. Unequal distribution of some factor in space generates vector field of force.
This “global factor” is called a “morphogenetic field,” which can be described in terms of a field of force. The basic idea of the morphogenetic field theory and the modern conception of positional information were first formulated clearly by Hans Driesch in 1894. He stated that prospective developing of an embryonic cell is a function of its position in the whole organism. The field governs body development and is an underlying principle of organism construction. Morphogenetic field is a result of initial heterogeneity of the fertilized egg or bud. The concentration gradient of molecules and fracturing of media into heterogeneous elements renders the process of transportation of the matter, energy, and information and leads to development of a vector field of force (Fig. 3). A living substrate and morphogenetic field entail a set of local functions on this substrate that are inextricably bound to and cannot exist without each other. In other words, morphogenetic fields immanently belong to the biological substrate. The field of force emerges in a developing organism due to its original heterogeneity, and this field imposes heterogeneity onto the space surrounding the organism, laying the groundwork for the further development of a complex structure. The heterogeneity of a space surrounding the developing organism is characterized by point-to-point changes of particular characters on that space. The value of these characters at some point is called a local order of the field. Local orders over the entire morphogenetic space are united into an integral order. Functional connection between local and integral orders is a positional information of given morphogenetic field. The area of a space, in which the local orders at all points have the same value, is called an equipotential surface. The initial and final states are connected by a trajectory called creod. The final structure at the end of creod is an attractor or dynamically preformed morph (DPM).
Thus, if \(P\) is a value of some character determined by the position in space, \(x\) a coordinate in this space, and \(t\) a time coordinate, then the existence of morphogenetic field means that there is a relation \( P = f(x,t) \). For example, let \(T\) be the distribution of temperature along some area. The local order of this field is described by the equation:
\[ \frac{\partial T}{\partial t} = a^2 \Delta T + F.\]
The integral order here is an integral of this equation. Positional information is a process of integration of this equation. The solution (integral) of equation is called a dissipate structure. Thus, the dissipate structure is an integral order of the field.
One of the main innovations of modern thermodynamics is an idea that different causes can result in the same effect or state of a developing system. Such a state of dynamic equilibrium is called attractor. All trajectories of possible system developmental pathways converge on it. Thus, attractor is a space of all possible states of the system. System can enter this space, but cannot leave. Non-linear system, such as organism, may have several attractors. In this case, each attractor has a basin. Basin is an area in space that all trajectories which start in this area end up in the attractor. Basins of different attractors are separated by a narrow borderline called bifurcation. When the system state is close to this border, its behavior is chaotic, but inside the basin it moves very predictably towards the attractor and sooner or later reaches it (Fig. 4).
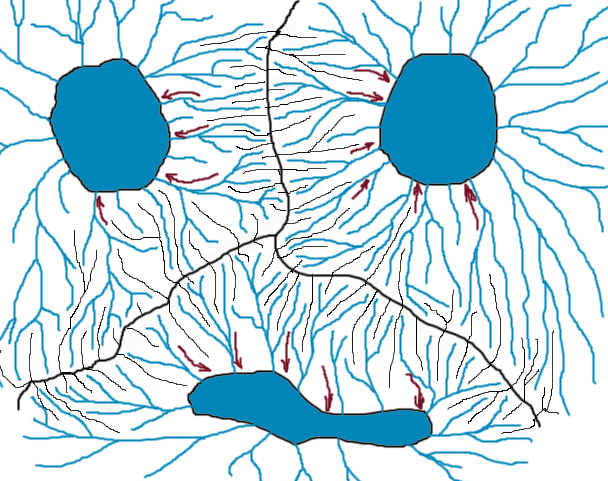
Figure 4. Attractors, basins, and bifurcations. Like lakes collect water of all rivers from its basin, attractors collect all states of the system that fall into its orbit.
When a dynamic system is under the stress, for example by increase of energy flow through it, the number of its attractors tends to increase. Thus, increase of chains of chemical reactions complexity that increased stability and effectiveness of transfer of energy through the system causes fracturing of final ends of metabolic pathways (attractors). Very probably, the most abundant living forms are under the stronger pressure (stress), then less numerous. For example, sexual dimorphism results from increase of stress on taxon. It may be caused by increase of basic metabolic rate of organisms, and as a result of that increase of energy flow. On the other hand, less numerous organisms are in a stable equilibrium, from which they will not move anywhere until stress level is low.
Once upon a time, the universe came to life; it continues to develop and grow more complex, while preserving its unity. It is impossible to imagine an absolutely chaotic world, where nothing is stable, no forces govern their interactions among entities that constitute this world. Even in the near-chaos systems there are some organizing forces, whose activity lead to the development of a future order. Decrease of entropy in an open system that is not in a state of equilibrium spurs this system toward self-organization. So, the world, most likely, has an internal, immanent order. In the process of the universe’s development, from the Big bang and up to the present, this order changes. At first, only physical laws compelled the universe to expand. Elementary particles brought to life new physical laws, which in turn led to the emergence of atoms. The occurrence of life on Earth is only one small step in the infinite unrolling of this primordial order, which governed the world from the very beginning. Being a complex system in a state of non-equilibrium, the universe from the very beginning had the ability of spontaneous self-organization: a fundamental property of complex systems.
Self-organization term was proposed by Ashby to indicate a machine that is “determinate and yet able to undergo spontaneous changes of internal organization” (Ashby, 1947; p. 125). Self-organization is a process of creation a macroscopic pattern. This pattern is emergent, it cannot be deduced from even a full knowledge of the lower-level components and the nature of the interactions among them. In self-organized systems “the whole is more than the sum of its parts” (Aristotle, 1984; p. 1045). New properties must arise solely from within the system, and not generated by interference or other external forces. It is difficult to identify self-organization by simple definition, but there are some most significant properties that are characteristic to it: 1) positive feedback as one of the forces driving system development; 2) negative feedback as a stabilizing force; 3) stochasticity and randomness that generate diversity of forms.
The evolution of the self-organizing system drives it toward increasing complexity by dividing of its primarily almost homogeneous structure into separate subsystems, each of which has particular characteristics and specific role in the whole system. This ensures its stability and decreases entropy due to an increase of structural complexity. This is a law of complex systems' development, which leads to progressively increasing internal structural diversity.
On the other hand, constantly dividing on particular parts evolving system remains united in a whole. Integration is an intrinsic property of the evolutionary process. Thus, systems with higher complexity, together with increase tendency to fracturing into subsystems, show an increase of their integrity. This unity arises within growing hierarchic organization and a complex system of feedbacks on every hierarchical level. Consider, for example, a school of fish containing thousands individuals that move in ocean water like a one body, turning in unison. This behavior is not encoded within each individual, nor is there a leader or small group of individuals directing the movement of the school. It arises from reaction of every individual fish to movements of their immediate neighbors, and, as a result of such local interactions, the group-level pattern of activity emerges spontaneously. Fish react by changing of heading by maintaining a constant distance with neighbors in order to swim away from a predator or to avoid crashing into neighbors. Let it be a parameter \(0 \le r \le 1\), which determines the degree of correlation of activity among individuals. It is easy to see that if \(r\) is high (close or equal to 1) than the movement of one single individual firmly causes a change in movements of most or all its neighbors. Such organization will “behave rigidly” and cannot be classified as self-organized. On the other hand, if \(r\) is very low, the movements of particular fish will cause little or no change in the school. Thus, there are low and high thresholds of parameter \(r\) (level of interaction between elements of the system) that define the range within which self-organization exists. The increase in diversity of such affecting interactions between elements increases ability of the system to self-organization and lead to development of hierarchical multilevel organized system. For example, let it be parameters: \(r\), \(s\), and \(t\) responsible for some special interaction between elements, and all of them vary from 0 (there is no interaction) to 1 (interaction is deterministic). If every element of the system at one moment can react only on one particular parameter and there is a priority of reaction on them: say, at first element reacts on parameter \(r\), than \(s\), and only after them all on parameter \(t\), then such a hierarchy of reactions will lead to the development of a hierarchy of positive and negative feedbacks that will correspond to hierarchy in organization of self-organizing system. Definitely, we can say that evolution of complex systems is founded on two basic processes: differentiation of the whole into parts and integration them into one functional unity. Both these processes are reciprocal and one doesn't exist without the other. We can say that: 1) life is an ability for self-organization; 2) life emerges everywhere where there are conditions for self-organization.
So, what we learn from the above? Life emerges everywhere where there exists an unequal distribution of matter and/or energy. The Developing Universe creates such opportunities and their number seems to grow. The Universe as a system has fundamental property - ability for self-organization. This means that Life is an intrinsic property of the Universe and we can say that the evolution of Life is a part of Universe development process. It sounds poetic, but we can say that the Universe itself is alive. And every celestial body that has at least two media (for example, liquid and gas) tends to develop at least some elements of living nature. How advanced are these forms is another question.