2.1 The Kepler problem

We begin by considering the Kepler Problem; the scattering process of two point-like masses due to mutual gravitational interaction.

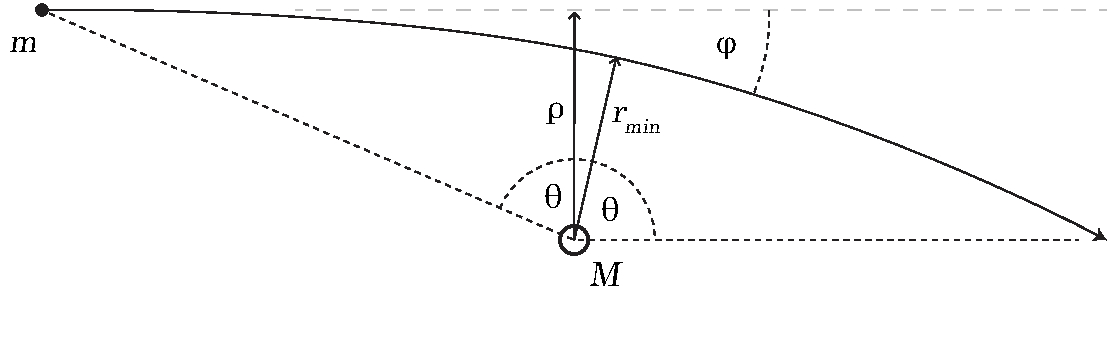
Figure 1: Scattering of mass \(m\) by a heavy target \(M\).

This process can be described by the change in relative velocity of the two masses \(m\) and \(M\) (or just the change in velocity of \(m\) if \(M \gg m\)). If we exclude external influences, the center-of-mass velocity of the system is unchanged. \begin{equation}\tag{1} \begin{array}{l} \Delta v_\parallel = -v + v\cos \phi,\\ \Delta v_\perp = v\sin \phi. \end{array} \end{equation} Here \(\vec{v} = \vec{v}_1-\vec{v}_2\) is relative velocity, \(\Delta \vec{v}\) is the change in relative velocity, and \(\phi\) is the angle of deflection, see Fig. 1.

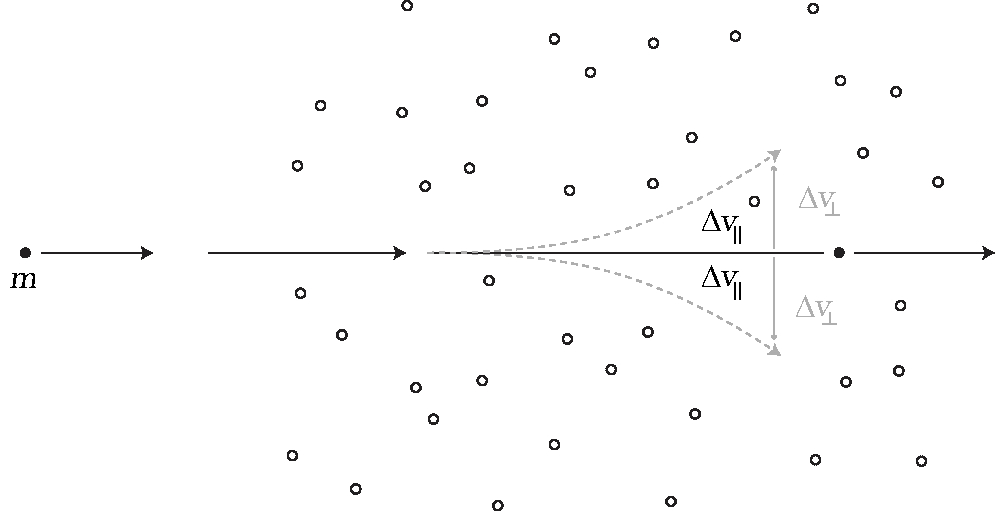
Figure 2. When moving through a uniform field, the parallel components of velocity are summed, and the perpendicular components are canceled.

Assuming a uniform distribution of stars in the field, changes in the perpendicular velocity component cancel out, see Fig. 2. From now on only the parallel velocity component is of interest. The scattering angle \(\phi\) relates to the direction of closest approach between the stars, with the corresponding angle \(\theta_0\) shown in Fig. 1. Now, with the help of \begin{equation}\tag{2} \phi = 2\theta_0 - \pi, \end{equation} we are able to define the change in velocity in terms of \(\theta_0\) as \begin{equation}\tag{3} \Delta v_\parallel = -2v \cos^2 \theta_0. \end{equation} The solution of the Kepler Problem is well known ‐ it relates the distance between two colliding bodies \(r\) with the polar angle \(\theta\) as \begin{equation}\tag{4} r = \frac{p}{1+e\cos\theta}. \end{equation} Here \(p\) is the conic parameter and \(e\) is the eccentricity. Using this solution of the Kepler Problem (4) we can define angle \(\theta_0\) and the corresponding change in velocity as \begin{equation}\tag{5} \cos\theta_0 = -\frac{1}{e}, \mbox{ when } r \rightarrow \infty \end{equation} and \begin{equation}\tag{6} \Delta v_\parallel = -2v\frac{1}{e^2} = -2v \frac{1}{1+\frac{v^2 L^2}{k^2}}. \end{equation} For eccentricity we used the known expression \begin{equation}\tag{7} e = \sqrt{1+\frac{v^2L^2}{k^2}}, \end{equation} where \(k = G m_1 m_2\) is the strength of the gravitational interaction, \(L = \mu \rho v\) is the relative angular momentum (with the impact parameter labeled as \(\rho\), see Fig. 1), and \(\mu = m_1m_2/(m_1+m_2)\) is the reduced mass of the system.

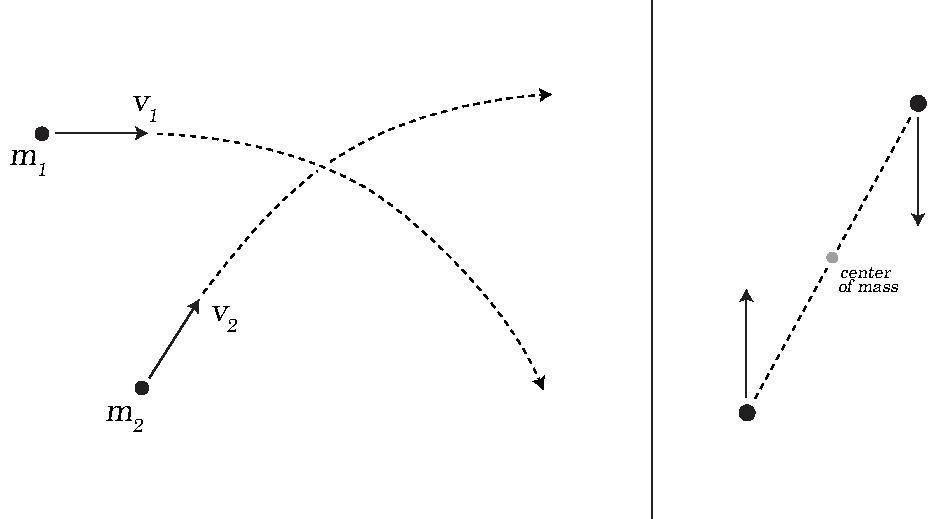
Figure 4: Center-of-mass and relative velocities.

The solution of the Kepler Problem allowed us to derive Eq.(6) without serious effort. From here, we could find the individual velocities of the scattering stars. This can be done using the following transformation (Fig. 3 may help in visualizing it)

\begin{equation} \vec{v}_1 = \vec{V}_{com} + \frac{m_2}{m_1+m_2} \vec{v},\tag{8} \end{equation}

\begin{equation} \vec{v}_2 = \vec{V}_{com} - \frac{m_1}{m_1+m_2} \vec{v},\tag{9} \end{equation}

where \(\vec{v}_1\) is the velocity of \(m_1\), \(\vec{v}_2\) is the velocity of \(m_2\), the center-of-mass velocity \(\vec{V}_{com}\) does not change during the scattering, and \(\vec{v}\) is the relative velocity.

Let's assign \(m_1\) to the passing star and \(m_2\) to the target. The change in \(\vec{v}_1\) can be related to the change in relative velocity \(\vec{v}\). Using Eqs.(6) and (8) we get \begin{equation}\tag{10} \Delta v_{1\parallel} = -2v \left( \frac{m_2}{m_1 + m_2} \right) \left( \frac{1}{1+\frac{\rho^2 v^4}{G^2(m_1 + m_2)^2}}\right), \end{equation} where \(v\) is the relative velocity, and \(\rho\) is the impact parameter.

2.2 Dynamical Friction Force

We can integrate over the stars from the field/galaxy assuming a certain distribution of masses \(m_2\) (targets) located at different positions \(\vec{r}\), moving with different velocities \(\vec{v}_2\). The number of targets can be expressed through the field concentration and corresponding elementary volumes \begin{equation}\tag{11} d N = n(\vec{r},\vec{v}_2) d^3r d^3v_2, \end{equation} where \(n(\vec{r},\vec{v}_2)\) is the generalized concentration of stars of mass \(m_2\) in the field/galaxy at point \(\vec{r}\) moving with velocity \(\vec{v}_2\). Note that \(\vec{r}\) is the position of \(m_2\) relative to the passing star \(m_1\).

The deceleration of the passing star due to interactions with \(dN\) targets can be calculated as \begin{equation}\tag{12} \frac{\Delta V_{\parallel}}{\Delta t} = \frac{\Delta v_{1\parallel}}{\Delta t} dN = n(\vec{r},\vec{v}_2) \Delta v_{1\parallel} 2 \pi\rho d\rho \frac{\Delta z}{\Delta t} d^3 v_2, \end{equation} where we assumed cylindrical symmetry and used the cylindrical coordinates for the volume: \(d^3 r = 2\pi \rho d\rho dz\). With some approximation, \({\Delta z}/{\Delta t}\) can be replaced with the relative velocity parallel component \(v_\parallel\).

The acceleration (12) can be integrated over the impact parameter \(\rho\), which can be done analytically if we assume that the concentration \(n\) is more-or-less constant near the position of the passing star: \(n(\vec{r},\vec{v}_2) \approx n(0,\vec{v}_2) \equiv n_0(\vec{v}_2)\), but goes to zero for large impact parameters \(\rho > \rho_{max}\). This could be, for example, the size of the galaxy. The integration over \(\rho\) gives us \begin{equation}\tag{13} \frac{\Delta V_\parallel}{\Delta t} = -2v v_\parallel n_0(\vec{v}_2) d^3 v_2 \left( \frac{m_2}{m_1 + m_2}\right) \int \frac{2\pi\rho d\rho}{1+\frac{\rho^2 v^4}{G^2(m_1 + m_2)^2}}, \end{equation} or, finally, with the logarithmic accuracy we get \begin{equation}\tag{14} \frac{\Delta V_\parallel}{\Delta t} = -4\pi G^2(m_1 + m_2)m_2 \ln\lambda\, \frac{v_\parallel}{v^3} n_0(\vec{v}_2) d^3v_2, \end{equation} where \(v_\parallel = {\Delta z}/{\Delta t}\) is the relative velocity in the direction of motion of the passing star (\(z\) was the relative coordinate), the cut-off parameter \(\Lambda\) is defined by the maximum impact parameter \(\rho_{max}\) after which the star field disappears: \(\Lambda \sim \rho_{max}v_c^2/Gm\), and \(v_c\) is the typical speed.

Now, if we multiply acceleration (14) by the mass of the passing star \(m_1\) we get the dynamical friction force on \(m_1\): \begin{equation}\tag{15} \vec{F}_{df} = -4\pi G^2(m_1 + m_2)m_1 m_2 \ln\lambda \int n_0(\vec{v}_2) \frac{\vec{v}_1 - \vec{v}_2} {\left| \vec{v}_1 - \vec{v}_2 \right|^3} d^3v_2, \end{equation} where we have substituted the relative velocity with: \(\vec{v}=\vec{v}_1-\vec{v}_2\).

For further calculation we need to assume a certain distribution of stars in the field over velocity, \(n_0(\vec{v}_2)\). For example, one could pick a Maxwell distribution. In our research, it would be sufficient to estimate the dynamical friction force (15) for a very heavy passing star: \(m_1 \gg m_2\). For an estimation, the concentration \(n_0\) can be replaced with the density of the target stars \begin{equation}\tag{16} \rho \sim m_2 \int n_0(\vec{v}_2) d^3 v_2, \end{equation} where \(\rho\) is the average density of the field (galaxy) at the location of the passing star (so \(\rho = \rho(r)\) is a function of the passing star position). This gives us a rough estimation of the force; \begin{equation}\tag{17} F_{df} \sim 4 \pi G^2 m_1^2 \rho(r) \frac{\ln \Lambda}{v_c^2}, \end{equation} where \(G\) is the universal gravitational constant, \(m_1\) is the mass of the passing star, \(\rho\) is the density of the field, \(v_c\) is the typical speed, and \(\Lambda\) is the cut-off parameter. For a more accurate integration of Eq.(15) the Gauss theorem can be applied. We can assume spherical symmetry for the velocity distribution \(n_0(\vec{v}_2)\). In this case, the velocities in the star field exceeding that of the spiraling body do not contribute to the dynamical friction force, something of particular interest.

2.3 Orbital Decay of a Heavy BH

We can determine the density profile formula, \(\rho = \rho(r)\) needed to calculate the dynamical friction force (17). In the case of spherical symmetry, the centripetal acceleration of a star moving around a galactic center is defined by the total mass enclosed by the star's orbit (another sample application of the Gauss Theorem!), \begin{equation}\tag{18} \frac{v^2}{r} = G \frac{\int^r \rho(x) 4\pi x^2 dx}{r^2}. \end{equation} Taking the orbital speed \(v\) as constant (due to the flattening of the rotational curves) we get \begin{equation}\tag{19} \frac{1}{r}{\int^r \rho(x) x^2 dx} = constant. \end{equation} It should be noted that our estimate will not take into account that rotational curves are not flat all the way to the center, but still it gives a sufficient enough estimation for the galactic density. Accepting (19), we can see that the corresponding density profile decreases with distance as \(\sim 1/r^2\), stated more accurately, \begin{equation}\tag{20} \rho(r) = \frac{v_c^2}{4 \pi G r^2}. \end{equation} We can now use Eq.(20) and the dynamical friction force (17) for a heavy passing star of mass \(M\) (in our case a heavy BH) moving though a field of stars. The dynamical friction force can be approximated as \begin{equation}\tag{21} F_{df} \sim 4 \pi G^2 M^2 \rho(r) \frac{\ln \Lambda}{v_c^2}. \end{equation} Substituting Eq.(20) into Eq.(21) we can get the following final expression for the dynamical friction force \begin{equation}\tag{22} F_{df} \sim \ln \Lambda \frac{G M^2}{r^2}. \end{equation} The orbital decay time of a heavy BH can be described in terms of orbital radius, orbital speed, the mass of the BH, and the cut-off parameter \(\Lambda\) discussed above. We can estimate the decay time as the ratio of the star's angular momentum, \(L\), to the torque, \(\tau\), exerted on the star by the dynamical friction force: \begin{equation}\tag{23} t \sim \frac{L}{\tau}=\frac{r M v_c}{r F_{df}} = \frac{M v_c}{F_{df}}. \end{equation} Finally, the decay time simplifies to \begin{equation}\tag{24} t \sim \frac{v_c r^2}{G M \ln \Lambda}. \end{equation} For an estimation, we chose a BH equivalent to \(10^8\) solar masses, \(M = 10^8\,M_\odot = 2\times 10^{38} kg\), with an orbital speed \(v_c = 200\,km/s = 2\times10^5\,m/s\), an orbital radius of \(r \sim 10\,kpc = 3.1\times10^{20}\,m\), and a cut-off parameter of \(\ln \Lambda \sim 7\). The universal gravitational constant \(G=6.67\times10^{-11}\,N m^2/kg^2\). Using these values we get the following estimation for the decay time \begin{equation}\tag{25} t \sim \frac{2\times10^5\cdot (3.1\times10^{20})^2 }{6.67\times10^{-11}\cdot2\times 10^{38}\cdot 7} \approx 2\times 10^{17}\,s = 6.5\times 10^9\,yr. \end{equation} At around 7 billion years, our estimate is comparable to the life-time of the universe. The corresponding mass dependence may looks like \begin{equation}\tag{26} t \sim 10^{18} \frac{M_\odot}{M} \mbox{ years}. \end{equation}