As part of their Honors “General Physics I” class, LaGuardia students Camille Enderlin and Lenin Nolasco conducted research on the processes that dictate the size of Neutron Stars and White Dwarfs.
The project was conducted under the supervision of Dr. Roman Senkov.
Other research projects done by students in the Physics Honors courses: “Orbital Decay of a Massive Black Hole”, “Atomic Nuclei and Pairing Correlations”, and “Computer Modelling of Physical Systems”.
Download this article: pdf (468Kb)
In this research, we explored the ways in which pressure, due to gravity and Fermi-Gas, contributes to the unique dimensions of Neutron Stars and White Dwarfs. We found that the typical radius of a Neutron Star is approximately 10 km, and the typical radius of a White Dwarf is approximately 8,000 km.
White Dwarfs and Neutron Stars are great examples of extremely dense collections of matter in the universe. Both are formed by the collapse of stars. The density and pressure found in both these stellar objects is much greater than anything that could be reproduced in a laboratory, so the measurements found by studying these objects provides information about physics fundamentals within such extreme environments.
White Dwarfs are formed by the collapse of low-mass stars and are composed of electron degenerate matter. They are the left-over core remnants of low mass stars that no longer sustain nuclear fusion. Within the layers of a main sequence star, Hydrogen is fused into Helium, and then Helium is fused into Carbon. Increased pressure caused by the nuclear fusion inside the star causes layers to expand, and then the star becomes unstable and bursts. White Dwarfs are mostly carbon and are very hot, but not hot enough to fuse carbon into anything else. Without any more nuclear fusion happening inside the star to create an outward pressure, electron degeneracy pressure is what stops White Dwarfs from gravitational collapse. The maximum mass of a white dwarf is known as the Chandrasekhar limit, which is \(1.44 M_\odot\), where \(M_\odot \approx 2\times10^{30}\,kg\) stands for the solar mass.
The next densest collection of matter after a White Dwarf is a Neutron Star. Neutron Stars are essentially very dense balls of neutrons. The only stellar object more dense would be a black hole. Neutron stars result from the collapse of massive stars, and due to their high mass, the compression due to gravity surpasses that of White Dwarfs. In Neutron Stars, electrons and protons get fused together creating neutrons. Neutron degeneracy pressure is what keeps Neutron Stars from collapsing even further, as neutrons cannot be compressed indefinitely.
In this paper we aim to explain the mass-radius relation of White Dwarfs and Neutron Stars by breaking down the various aspects of density and pressure, and providing calculations for the pressure due to factors such as gravity and Fermi gas. We will also utilize phase space to discuss Fermi level and provide equations regarding the number of states or particles in each object.
We aim to determine the minimum radius for White Dwarfs and Neutron Stars, which will be dictated solely by each star's mass. For simplicity, all of our equations will be made with the assumption that both White Dwarfs and Neutron Stars are uniform spherical distributions of matter. As the first step, we will determine the total energy of either a White Dwarf or a Neutron Star. To do so, we must add the energy due to gravitational interaction and the energy due to Fermi gas. Both energies are functions of start's radius \(R\) and star's mass \(M\): \begin{equation}\tag{1} E_{total}(R, M) = E_{Gravity} (R, M) + E_{Fermi-gas} (R, M). \end{equation} Pressure as a function of mass and radius is particularly interesting as both these stellar objects have limits in terms of how dense they can be before they release energy and become another object. A smaller radius results in higher pressure, and if the radius continues to shrink, the pressure grows and eventually results in explosion. As a result, the size of a star will stabilize when the pressure due to gravity is balanced out by the internal pressure due to the Fermi gas, and when the total energy (1) reaches its minimal value. To solve for the equilibrium radius of the star, we can establish the following equation: \begin{equation}\tag{2} 0 = \frac{d}{d R}\left[ E_{Gravity} (R, M)\right] + \frac{d}{d R} \left[E_{Fermi-gas} (R, M)\right]. \end{equation}
The gravitational energy as a function of the radius \(R\) and mass \(M\) can be written as \begin{equation}\tag{3} E_{Gravity} = -\frac{3GM^2}{5R}, \end{equation} where \(G=6.67\times10^{-11}\) Nm2/kg2 is the universal gravitational constant, \(M\) is the star's mass, and \(R\) is the star's radius. The 3/5 constant was obtained under assumption that both White Dwarfs and Neutron Stars are of uniform spherical distribution [1].
Fermi gas is the gas of fermions, which are identical particles of half-integer spin that obey the Pauli principle [2]. Spin is the angular momentum of elementary particles. Examples of fermions include neutrons, electrons, and protons. In quantum mechanics, a quantum state can have the minimum volume in the position-momentum space (commonly known as phase space), which is determined solely by the value of the Planck constant: \begin{equation}\tag{4} \mbox{“Phase space volume”} = \left\{ \begin{array}{ll} dx \cdot dp = 2\pi\hbar, & \mbox{in 1-D}\\ d^3 x \cdot d^3 p = \left(2\pi\hbar\right)^3, & \mbox{in 3-D} \end{array}\right., \end{equation} where \(\hbar = 1.055\times 10^{-34}\) Js is the reduced Planck constant [3]. The phase space helps us understand why radius is an essential component of energy in this circumstance. Phase space consists of all possible states of a system. In phase space, particles do not occupy random space, but rather are placed directly next to each other in a uniform distribution [4]. The Pauli exclusion principle is a quantum mechanical principle that states two or more identical Fermions cannot occupy the same quantum mechanical state (in our case, electrons for White Dwarfs and neutrons for Neutron Stars) can occupy the same quantum state. Consequently, equation (4) provides us with the maximum number of particles that can be accommodated within a star without violating Pauli's principle \begin{equation}\tag{5} N = 2 \int \frac{d^3x d^3p}{(2\pi\hbar)^3} = \frac{32\pi^2}{9} \frac{R^3 p_F^3}{(2\pi\hbar)^3}, \end{equation} here the factor 2 is due to spin (there are two spin states: spin up and spin down), while the star's radius \(R\) restricts the integration in space, and the maximum particle momentum \(p_F\) (commonly referred to as the Fermi momentum) restricts the integration in momentum space.
The number of Fermi particles in Eq.(5) can be found by dividing the mass of the star by the nucleon mass (either the mass of a neutron or a proton). For Neutron Stars, we take the mass of the star and divide it by the neutron mass. For White Dwarfs, we do the same but divide by two neutron masses, as due to their Carbon-12 composition, there is one electron per two nucleons. Consequently, Eq.(5) enables us to express the Fermi momentum as a function of the number of particles and later as a function of star's mass \begin{equation}\tag{6} p_F = \sqrt[3]{\frac{9\pi}{4}} \frac{\hbar}{R} N^{1/3}. \end{equation} We are mainly concerned with momentum and position, as our \(p_F\) will represent the maximum possible momentum of particles in the star. The Fermi level is defined by the number of particles to fit in a phase space and the star's radius.
As demonstrated in Eq.(6), a smaller radius will result in a greater maximum particle momentum and greater energy, leading to increased pressure inside the star. The energy due to the Fermi gas, as a function of the radius and number of particles, can be derived as follows: \begin{equation} \tag{7} E_{Fermi-gas}=\int \epsilon_p dN = 2 \int \epsilon_p \frac{d^3x d^3p}{(2\pi\hbar)^3}, \end{equation} where \(\epsilon_p = p^2/2m\) is term represents the energy of a single Fermi particle (in our case, it is simply kinetic energy). After integration, we obtain \begin{equation} \tag{8} E_{Fermi-gas}=\frac{9}{20} \sqrt[3]{\frac{3\pi^2}{2}} \frac{\hbar^2 N^\frac{5}{3}}{mR^2} \sim \frac{p^2_F}{2m} N, \end{equation} here \(N\) and \(m\) are the number of particles in the Fermi-gas and their mass: neutrons for Neutron Stars and electrons for White Dwarfs. The nummber of fermi particles can be related to the star's mass \(M\) and the nucleon mass \(m_n\) as \begin{equation} \tag{9} N = \eta \left( \frac{M}{m_n}\right), \end{equation} where prameter \(\eta\) represents the number of the fermi particles per nucleon: \(\eta_{NS}=1\) (Neutron Stars consist most of neutrons) and \(\eta_{WD}=1/2\) (inside White Dwarfs for two nucleons there is one electron, due to 12C composition).
We combined energy due to gravity and energy due to Fermi-gas to get the total energy of a star. The energy due to gravity is a function of radius and mass, whereas the energy due to Fermi-gas is a function of radius and the number of particles in the star.
Looking back at Eq. (1), we see that our total energy is the sum of the two energies, Eqs.(3) and (8), \begin{equation}\tag{10} E_{total}= - \frac{3GM^2}{5R} + \frac{9}{20} \sqrt[3]{\frac{3\pi^2}{2}} \cdot \frac{\hbar^2 N^\frac{5}{3}}{mR^2}. \end{equation} While Eq. (10) could be simplified, for the purpose of better visualizing the combination of energies we leave it as is. Insead, we created a plot for Neutron Stars and White Dwarfs using Eq.(10).
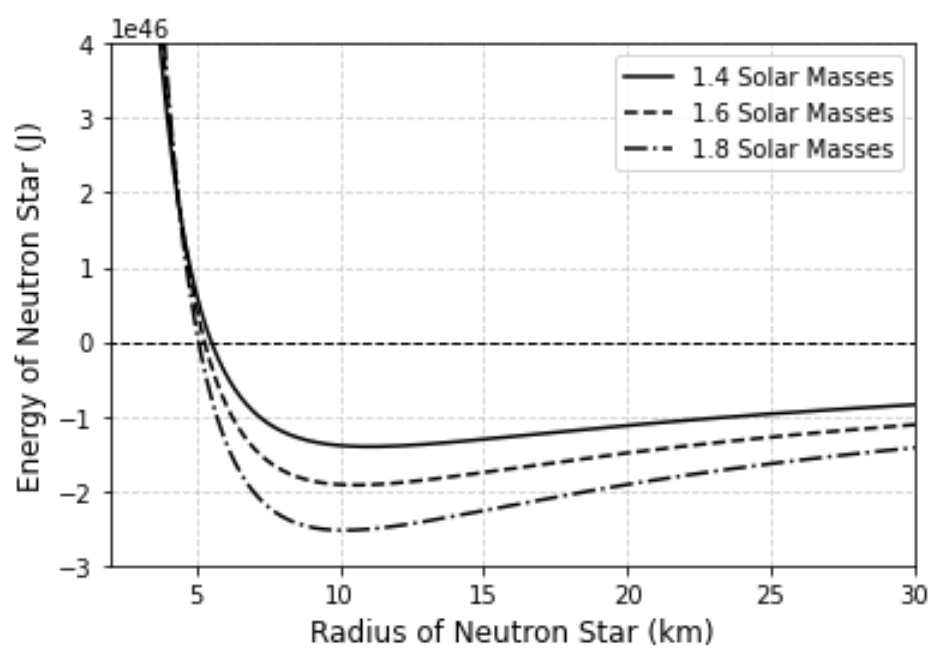
Figure 1: The total energy of a Neutron Star as a function of the star radius. Different curves represent different star masses: solid - 1.4 Solar mass, dashed - 1.6 Solar mass, and dashed-dotted - 1.8 Solar mass.
Figure 1 shows the total energy of three Neutron Stars with different solar masses as a function of radius. Looking at the minimum energy for each star, we can see that their radius is around the range of 10 km.
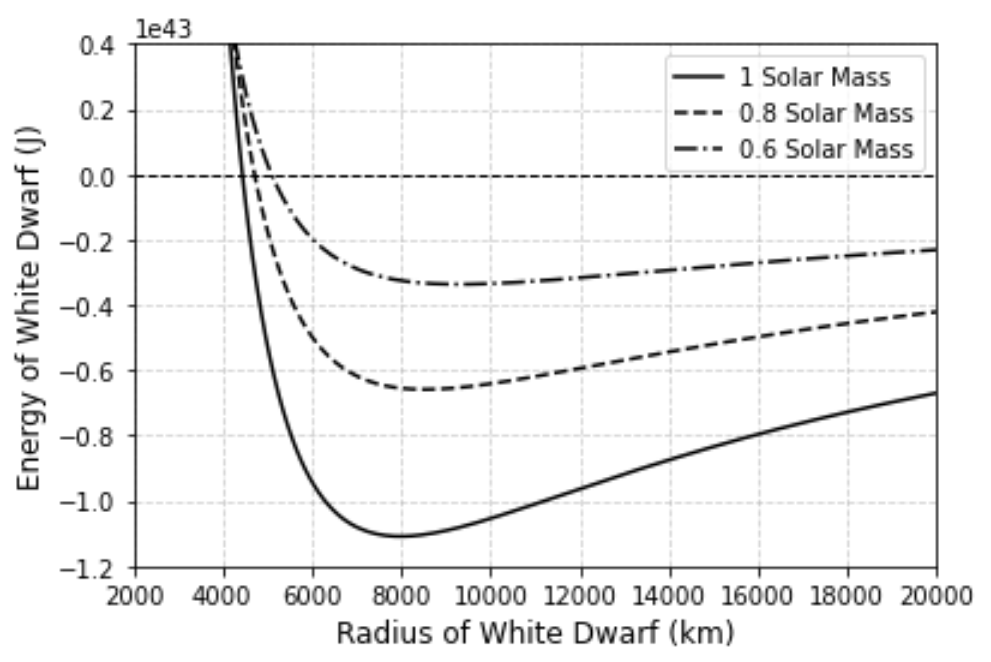
Figure 2: The total energy of a White Dwarf as a function of the star radius. Different curves represent different star masses: solid - 1.0 Solar mass, dashed - 0.8 Solar mass, and dashed-dotted - 0.6 Solar mass.
Similarly, Fig. 2 shows the total energy of three White Dwarfs with different masses as a function of radius. Looking at the minimum energy for each star, we see that their radius is around 8,000 km. These graphs show that the radius of the star is a major component of the overall energy.
We then looked at the equations for radius for Neutron Stars and White Dwarfs. The masses \(m\) in each equation are different because the mass of the Fermi particle responsible for repulsion in Neutron Stars and White Dwarfs are different. The equation for the radius of a Neutron star is \begin{equation}\tag{11} R_{NS} = \left(\frac{9\pi}{4}\right)^\frac{2}{3} \frac{\hbar^2}{G m_n^\frac{8}{3} M^\frac{1}{3}} , \end{equation} where \(m_n\) is the mass of a neutron and \(M\) is the mass of the star. Neutron Stars are composed of almost entirely neutrons, the mass any other particles are negligible and thus not considered in our equation.
The equation for the radius of a White Dwarf can be written as \begin{equation}\tag{12} R_{WD} = \left(\frac{9\pi}{4}\right)^\frac{2}{3} \frac{\hbar^2}{G m_e (2m_n)^\frac{5}{3} M^\frac{1}{3}}. \end{equation} For White Dwarfs, the main difference in comparison to Neutron Stars is that we are considering the mass of electrons rather than neutrons when calculating the radius. White dwarfs contain carbon, specifically Carbon-12, which is made of 6 protons, 6 neutrons, and 6 electrons. White Dwarfs are composed of electron degenerate matter, which contributes to the electron degeneracy pressure that keeps White Dwarfs from collapsing further into a Neutron Star or black hole [5]. When we plugged the numbers on the radius equation for Neutron stars, assuming a star of \(1.4M_\odot\), we get a radius of 11 kilometers, which is around the value of radius that we got from looking at the graph of energy of Neutron Star. Similarly, when we plugged in the numbers on the radius equation for a White Dwarf, assuming a star of \(1M_\odot\), we get a radius of about 7,200 kilometers, which is around the value of radius that we got from looking at the graph of energy of White Dwarf.
In conclusion, we can observe that the size of White Dwarfs is determined by electrons, which, due to the Pauli principle, resist being tightly compressed. Conversely, the size of Neutron Stars depends on neutrons. Electrons are about 2,000 times lighter than neutrons, so gravity more readily accelerates them and applies compressive forces. Consequently, compared to the heavier neutrons, electrons, at the same momentum, will possess higher energy, providing a stronger outward pressure. This results in the typical size of White Dwarfs being about 1,000 times larger than that of Neutron Stars: \begin{equation}\tag{13} \frac{ R_{WD}} {R_{NS}} \sim \frac{m_n}{m_e} \sim 1,000. \end{equation}
[1] https://en.wikipedia.org/wiki/Gravitational_binding_energy.
[2] I.G. Kaplan, The Pauli Exclusion Principle: Origin, Verifications, and Applications, John Wiley & Sons, 2017; https://en.wikipedia.org/wiki/Pauli_exclusion_principle.
[3] https://en.wikipedia.org/wiki/Planck_constant.
[4] L. Cohen, “Generalized Phase-space Distribution Functions,” Journal of Mathematical Physics, 7 5 (1966), pp. 781-786.
[5] D. Koester and G. Chanmugam, “Physics of White Dwarf Stars,” Reports on Progress in Physics, 53 7 (1990), p. 837.