by Bibi Valenzuela and Joan Velasquez
This work was done by LaGuardia students Bibi Valenzuela and Joan Velasquez as a part of the Honors “General Physics I” class, Fall 2024. In this work, Bibi and Joan investigate the Tsiolkovsky Rocket Equation that describes the relationship between a rocket's changing mass and velocity during propulsion.
The research was conducted under the supervision of Dr. Roman Senkov.
Other research projects done by students in the Physics Honors courses: “Maupertuis's Principle and Its Analog in Quantum Mechanics”, “Orbital Decay of a Massive Black Hole”, “Atomic Nuclei and Pairing Correlations”, “Computer Modelling of Physical Systems”, “Lagrange Points in Binary Star Systems”, and “Unveiling Stellar Dimensions: An Exploration of Neutron Stars and White Dwarfs”.
Download this article: pdf (1012Kb)
A key concept in rocket physics, the Tsiolkovsky Rocket Equation describes the relationship between a rocket’s changing mass and velocity during propulsion. This article examines the derivation and application of the equation, emphasizing its significance in understanding the dynamics of rocket motion. Starting with momentum conservation, the derivation extends to account for gravity and time-dependent elements such as mass loss, velocity, and altitude. These concepts are applied to analyze and compare the performance of modern rockets, including NASA’s SLS, the United Launch Alliance’s Atlas V, and SpaceX’s Falcon 9, over time. The results illustrate how fuel consumption decreases mass, driving increases in both velocity and altitude.
Initially created as weapons of war, rockets have evolved into essential tools for space exploration. This transformation was significantly influenced by Konstantin Tsiolkovsky, a pioneer in rocket science, who formulated the Tsiolkovsky Rocket Equation. This equation defines the exponential relationship between a rocket’s mass and the velocity it can achieve through the expulsion of gas. As rockets burn fuel and release exhaust gases, their mass decreases, allowing for greater acceleration.
The ideal rocket equation is formulated as follows [1]: \begin{equation}\tag{1} m = m_0 e^{-\frac{\Delta v}{u}}, \end{equation} where \(\Delta v\) represents the change in velocity the rocket needs to achieve, \(u\) is the exhaust velocity – the speed at which the fuel gases are expelled from the rocket engine (a higher exhaust velocity results in greater thrust), \(m_0\) is the rocket’s initial mass, including fuel, and \(m\) is the rocket’s final mass after the velocity change occurs.
This article delves into the physics behind the rocket equation, exploring its complexities and how it serves as a crucial framework for modern space missions. Space exploration has not only driven the rapid development of rockets but also enabled satellite deployments that support communication, GPS, Earth observation, and scientific research. Over the past 50 years, global investments in rocket development have totaled between 500 billion and 1 trillion USD.
Notably, Elon Musk, founder of SpaceX, has championed deep space exploration – such as missions to Mars – with an emphasis on cost-effective solutions. His vision has spurred both public and private sector investment in the future of rocket development. The evolution of rockets, from military weapons to SpaceX innovations, highlights a pivotal shift in space exploration. Through Tsiolkovsky’s rocket equation, we continue to advance propulsion technology, expand our capabilities, and inspire future explorers of the cosmos.
Let us derive Tsiolkovsky’s Rocket Equation (see, for example, [2]). We begin with the fundamental principle of conservation of momentum, taking into account the rocket’s decreasing mass over time as it expels fuel. As the rocket ejects fuel backward, it gains an equal amount of forward momentum, generating thrust that propels the rocket forward. This process is consistent with Newton’s third law of motion.
The Tsiolkovsky Rocket Equation provides a deeper understanding by expressing a mathematical relationship among the rocket’s velocity change, the exhaust velocity, and the ratio of the rocket’s initial to final mass. The initial momentum of the rocket, \(p_i\), is expressed as \begin{equation}\tag{2} p_i = mv, \end{equation} where \(m=m(t)\) is the mass of the rocket and \(v=v(t)\) is the rocket's velocity at given time \(t\).
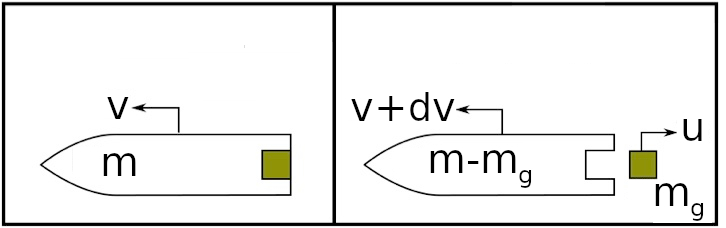
Figure 1: A rocket expels part of its mass to propel itself. The gas is expelled at velocity \(-u\) relative to the rocket, and at velocity \(v-u\) as observed from the laboratory frame.
The final momentum of the combined rocket–gas system can be expressed as, see Fig. 1, \begin{equation}\tag{3} p_f = (m - m_g)(v + dv) + m_g(v - u), \end{equation} where \(m_g\) is the mass of the gas expelled by the rocket, \(dv\) is the increase in the rocket’s velocity, and \(u\) is the velocity of the gas relative to the rocket.
Since momentum is conserved the initial and final momenta are set equal to each other: \begin{equation}\tag{4} mv = (m - m_g)(v + dv) + m_g(v - u), \end{equation} resulting in the following relation: \begin{equation}\tag{5} dv = -u \frac{dm}{m}, \end{equation} where we have replaced the mass of the expelled gas with the change in the rocket’s mass: \(m_g = -dm\).
One key insight from the equation above is that the change in velocity is directly proportional to the exhaust velocity and inversely proportional to the current mass. Moreover, integration plays a crucial role in deriving the total change in velocity, as this relationship must be integrated over the entire process of fuel consumption – from the initial to the final mass. \begin{equation}\tag{6} \int_{v_0}^{v} dv = -u \int_{m_0}^{m} \frac{dm}{m} \end{equation} Evaluating both integrals yields the following equation: \begin{equation}\tag{7} \Delta v = -u \ln \left( \frac{m}{m_0} \right). \end{equation}
Rearranging the equation to express \(m\) in terms of \(m_0\), \(\Delta v\), and \(u\), we obtain: \begin{equation}\tag{8} m = m_0 e^{-\frac{\Delta v}{u}}. \end{equation} This final form highlights how the rocket’s mass decreases exponentially as it gains velocity.
Let us consider the motion of a rocket in a gravitational field. Incorporating gravity into the rocket equation alters the relationship between mass, thrust, and velocity. Since gravity continuously acts on the rocket, it introduces a force that must be countered by thrust. This results in time-dependent factors that significantly influence the rocket’s trajectory and fuel consumption. When operating in a gravitational field with acceleration \(g\), the rocket equation (7) becomes: \begin{equation}\tag{9} \Delta v = -u \ln \left( \frac{m}{m_0} \right) - gt. \end{equation} This equation illustrates how the rocket’s velocity is affected by both the reduction in mass due to fuel consumption and the constant downward force of gravity over time. Here, \(g\) is the acceleration due to gravity (approximately \(9.81\, \mathrm{m/s^2}\) on Earth), and \(t\) is the time elapsed since launch. The negative sign in the \(-gt\) term indicates that gravity opposes the rocket’s thrust, thereby reducing its net velocity over time.
Building upon the effects of mass loss and gravitational force on a rocket’s motion, it is important to consider the role of time in these dynamics. By expressing mass as a function of time, we have: \begin{equation}\tag{10} m(t) = m_0 - |\dot{m}|t, \end{equation} where \(\dot{m}\) is the rate at which the rocket burns fuel. Substituting this expression into equation (8) allows us to integrate over time and derive the velocity as a function of time: \begin{equation}\tag{11} v(t) = -u \ln\left(1 - \frac{|\dot{m}|}{m_0}t\right) - gt. \end{equation}
To extend these calculations, we introduce the concept of thrust, defined as \(f = |\dot{m}| u\), where \(f\) is the thrust force produced by the rocket’s engines. This expression shows how rockets generate the force needed to overcome gravity and achieve targeted acceleration.
Using this, \(f\) can be substituted into equation (10) to yield: \begin{equation}\tag{12} v(t) = -u \ln\left(1 - \frac{f t}{m_0 u}\right) - gt. \end{equation}
This modified equation balances the upward acceleration generated by propulsion with the downward pull of gravity, offering a clearer picture of the rocket’s changing velocity over time as it burns fuel: \begin{equation}\tag{13} \frac{v(\tau)}{u} = -\ln\left(1 - \frac{f}{m_0 g} \cdot \frac{g t}{u} \right) - \frac{g t}{u} = -\ln\left(1 - n \tau \right) - \tau, \end{equation} where the thrust-to-weight ratio (\(n = {f}/{m_0 g}\)) measures the rocket’s thrust relative to its weight, determining its ability to overcome gravity; the dimensionless time ratio (\(\tau = {g t}/{u}\)) scales time by gravitational acceleration and exhaust velocity, enabling a simplified analysis of rocket motion. Figure 2 visually represents this equation, showing the rocket’s velocity as a function of time in a constant gravitational field. Remarkably, at \(\tau = 1/n\), the rocket exhausts all its fuel and, according to the idealized model, reaches infinite velocity.
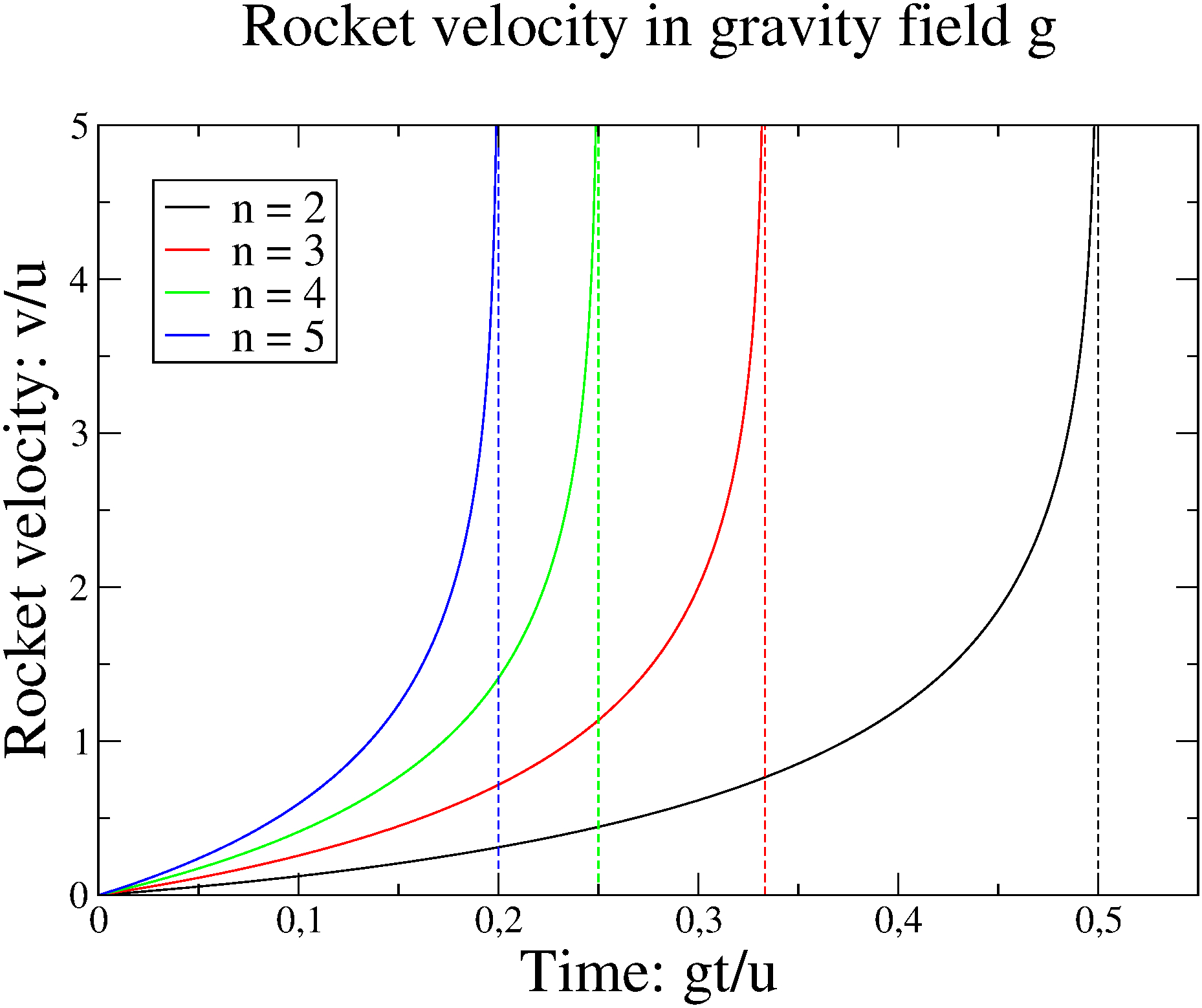
Figure 2: Velocity of a rocket as a function of time in a constant gravitational field \(g\), under constant thrust characterized by the thrust-to-weight ratio \(n\), for values n = 2, 3, 4, and 5. The vertical dashed lines indicate the moments when the rocket exhausts its fuel, corresponding to the condition \(m = m_0 - |\dot{m}|t\). Higher values of \(n\) lead to faster acceleration and earlier fuel depletion.
When a rocket launches, its height over time is influenced by the engine’s thrust propelling it upward, Earth’s gravity pulling it downward, and the continuous loss of fuel, which reduces the rocket’s mass as it ascends. Because the rocket’s mass changes during flight, calculating its exact height at any given moment is not straightforward. Engineers apply the Tsiolkovsky Rocket Equation to determine how the rocket’s velocity evolves as it loses mass. By analyzing this velocity as a function of time, we can estimate the rocket’s altitude. For simplified scenarios, basic physics provides a rough approximation, but real-world missions require more detailed modeling.
From Tsiolkovsky’s Rocket Equation, the velocity at any time \(t\) is given by: \begin{equation}\tag{14} v(t) = -u \ln\left(1 - n \frac{g t}{u}\right) - g t. \end{equation}
To determine height as a function of time, we integrate the velocity: \begin{equation}\tag{15} h(t) = \int v(t)\, dt. \end{equation}
To integrate the logarithmic part of Eq. (14), we use the substitution \(w = 1 - n \tau\), which gives \(dw = -n\, d\tau = -{n g}/{u}\, dt\). This transforms the height integral into: \begin{equation}\tag{16} h(t) = \frac{u^2}{n g} \int \ln(w)\, dw - \frac{g t^2}{2}. \end{equation} Now we integrate Eq. (16) by parts: \begin{equation}\tag{17} h(t) = \frac{u^2}{n g} \left[ w \ln(w) - w \right] \Big|_1^{1 - n \tau} - \frac{g t^2}{2}. \end{equation} Evaluating the integrals yields an expression for \(h(t)\) in terms of \(n\), \(u\), and \(\tau = {g t}/{u}\): \begin{equation}\tag{18} h(t) = \frac{u^2}{n g} \left[ (1 - n \tau) \ln(1 - n \tau) - (1 - n \tau) + 1 \right] - \frac{g t^2}{2}, \end{equation} or equivalently, \begin{equation}\tag{19} h(t) = \frac{u^2}{n g} \left[ (1 - n \tau) \ln(1 - n \tau) + n \tau \right] - \frac{g t^2}{2}. \end{equation}
Expressing height as a function of the dimensionless time \(\tau\), we get: \[ h(\tau) = \frac{u^2}{n g} \left[ (1 - n \tau) \ln(1 - n \tau) + n \tau \right] - \frac{u^2 \tau^2}{2 g} = \] \[ = \frac{u^2}{2 g} \left[ \frac{2}{n} \left[ (1 - n \tau) \ln(1 - n \tau) + n \tau \right] - \tau^2 \right] = \] \begin{equation}\tag{20} = h_0 \left[ \frac{2}{n} \left[ (1 - n \tau) \ln(1 - n \tau) + n \tau \right] - \tau^2 \right], \end{equation} where \(h_0 = {u^2}/{2 g}\) is the characteristic height scale.
Figure 3 illustrates the altitude \(h/h_0\) of a rocket as a function of dimensionless time \(\tau = g t / u\) in a gravitational field. This formulation enables us to calculate a rocket’s altitude while accounting for fuel consumption (mass loss) and the downward pull of gravity. By carefully integrating the effects of thrust, gravity, and changing mass, we obtain a realistic model that describes the rocket’s trajectory. This result enhances our understanding of how these forces interact to shape the rocket’s path during ascent.
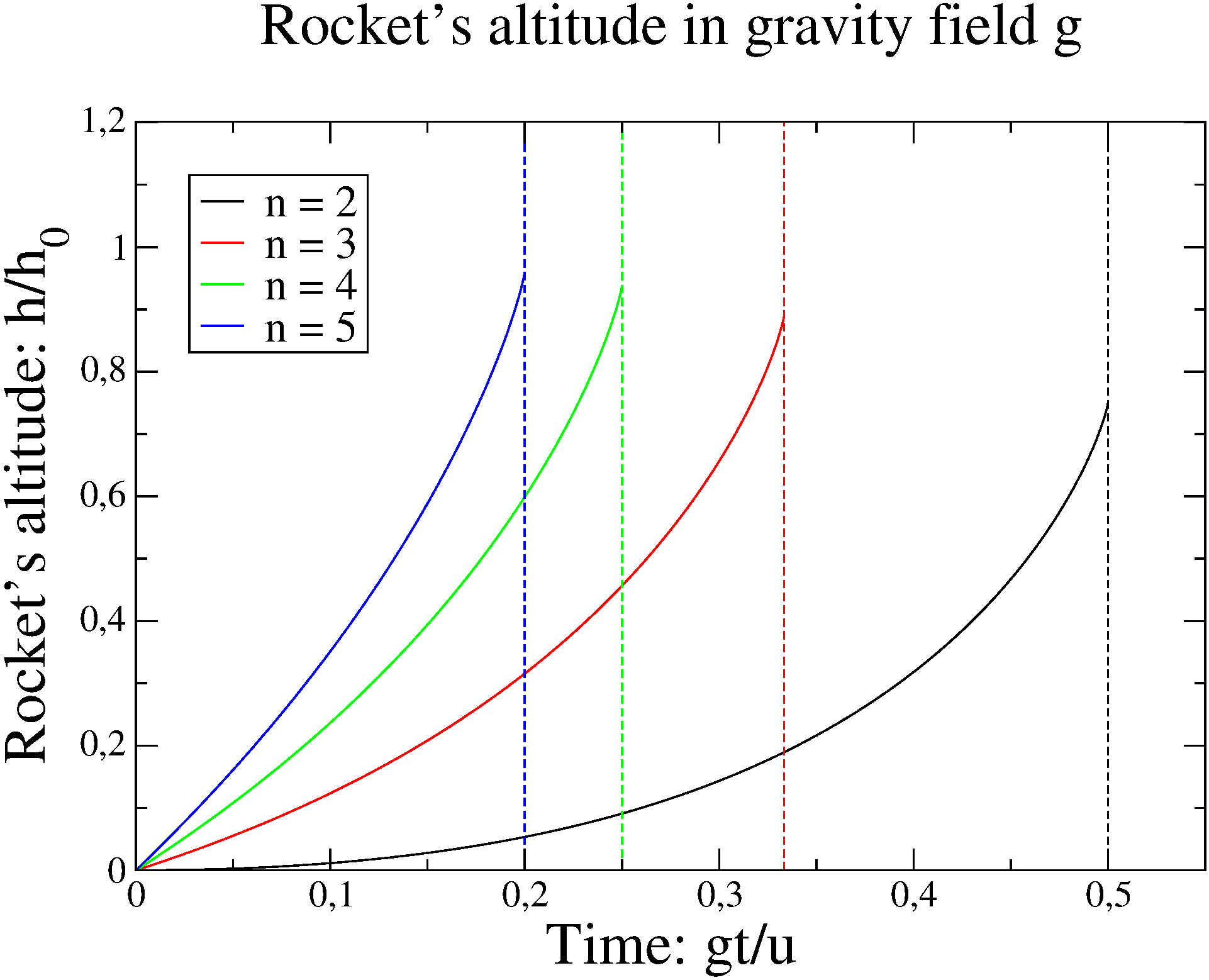
Figure 3: Altitude of a rocket $h$ as a function of dimensionless time \(\tau = g t / u\). The curves show the normalized altitude \(h / h_0\) for rockets with different thrust-to-weight ratios n = 2, 3, 4, and 5. The vertical lines indicate the moments when each rocket depletes its fuel. Rockets with higher \(n\) values gain altitude more rapidly but consume their fuel in a shorter amount of time.
This section applies the standard equations for mass, velocity, and altitude as functions of time to analyze the characteristics and performance of three well-known rockets: NASA’s Space Launch System (SLS), SpaceX’s Falcon 9, and the United Launch Alliance’s Atlas V. The table below presents the key parameters gathered for each vehicle.
| Specification | NASA SLS [3] | SpaceX Falcon 9 [4] | ULA Atlas V [5] |
|---|---|---|---|
| Height (m) | 98 | 70 | 62 |
| Launch Mass (kg) | 2,700,000 | 549,054 | 546,700 |
| Empty Mass (kg) | 190,000 | 40,000 | 23,297 |
| Stages | 2 | 2 | 2 |
| Thrust (kN) | 40,000 | 7,607 | 12,000 |
| Burn Time (s) | 480 | 397 | 240 |
| Exhaust Velocity (m/s) | 4,400 | 3,255 | 3,320 |
The total mass of a rocket at liftoff is referred to as the launch mass (\(m_0\)), while the empty mass represents the rocket’s mass after all propellant has been consumed. During flight, rockets typically operate in multiple stages. When the fuel in the first stage is depleted, that stage is jettisoned to reduce mass, allowing the next stage to continue the ascent more efficiently. Burn time – the duration for which an engine operates while consuming propellant – is a key factor in determining how long each stage can generate thrust.
Rocket thrust is a critical performance factor, with each vehicle employing specialized engines tailored to its mission. NASA’s Space Launch System (SLS) utilizes RS-25 engines, originally developed for the Space Shuttle, known for achieving high exhaust velocities. SpaceX’s Falcon 9 is powered by Merlin engines, which are optimized for reusability and cost-efficiency. The United Launch Alliance Atlas V features RD-180 engines, recognized for their reliability and high thrust capability.
Using the parameters provided in Table 1, we calculated the mass, velocity, and altitude of each rocket over time by applying the equations introduced earlier:
Mass over time: \(m(t) = m_0 - |\dot{m}|t = m_0 \left( 1 - n \tau \right)\)
Velocity over time: \(v(t) = u \left(-\ln(1 - n \tau) - \tau \right) \)
Height over time: \(h(t) = h_0 \left[ \frac{2}{n} \left[ (1 - n \tau) \ln(1 - n \tau) + n \tau \right] - \tau^2 \right]\)
The results of these calculations are summarized in Table 2, which presents the mass, velocity, and altitude of the three rockets at various times during their ascent.
| Time (s) | Mass (kg) | Velocity (m/s) | Altitude (m) | |
|---|---|---|---|---|
| Falcon 9 | 0 | 549,054 | 0 | 0 |
| 10 | 525,684 | 43.5 | 212.3 | |
| 20 | 502,314 | 93.4 | 891.1 | |
| 30 | 478,943 | 150.4 | 2,103.9 | |
| NASA SLS | 0 | 2,700,000 | 0 | 0 |
| 10 | 2,609,091 | 52.6 | 258.7 | |
| 20 | 2,518,182 | 110.5 | 1,069.8 | |
| 30 | 2,427,273 | 174.2 | 2,488.7 | |
| ULA Atlas V | 0 | 546,700 | 0 | 0 |
| 10 | 510,555 | 129.0 | 632.0 | |
| 20 | 474,411 | 274.7 | 2,635.4 | |
| 30 | 438,266 | 439.7 | 6,189.6 |
As expected, the mass of each rocket decreases over time due to fuel consumption, in accordance with the principles described by the Tsiolkovsky Rocket Equation (1). This reduction in mass is directly correlated with an increase in velocity, enabling the rockets to reach greater altitudes.
The Falcon 9 exhibits steady increases in both velocity and altitude, achieving a speed of 150.4 m/s and an altitude of 2.10 km at 30 seconds, with a reduced mass of 478,943 kg – demonstrating the vehicle’s smooth and controlled engineering. NASA’s SLS gains velocity and altitude more rapidly due to its greater mass and more powerful propulsion system, reaching 174.2 m/s and 2.49 km at the same time, with a mass of 2,427,273 kg. The Atlas V outperforms both, attaining 439.7 m/s and 6.19 km at 30 seconds, with a mass of 438,266 kg, showcasing its highly efficient propulsion.
This analysis highlights the fundamental role of mass loss in rocket performance, demonstrating how it contributes to increased velocity and altitude. It also lays the foundation for examining acceleration as a function of time, showing how mass and thrust shape velocity changes. Furthermore, it provides valuable insight into variations in kinetic and potential energy, as well as energy losses due to heat. Optimizing rocket design and improving fuel efficiency remain critical for the success of future space missions.
In conclusion, this research underscores the importance of the Tsiolkovsky Rocket Equation as a cornerstone of modern aerospace science. We sincerely thank our professor, Dr. Roman Senkov, for his guidance and encouragement throughout this project. His expertise and feedback were instrumental in helping us understand and apply these concepts. We also gratefully acknowledge LaGuardia Community College for providing the resources and support that made this study possible.
[1] NASA Glenn Research Center. Ideal Rocket Equation. https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/ideal-rocket-equation/
[2] OpenStax. Rocket Propulsion. In University Physics Volume 1. https://openstax.org/books/university-physics-volume-1/pages/9-7-rocket-propulsion
[3] NASA. SLS (Space Launch System) Block 1B. https://www.nasa.gov/reference/sls-space-launch-system-block-1b/
[4] SpaceX. Falcon 9. https://www.spacex.com/vehicles/falcon-9/
[5] United Launch Alliance. Atlas V Cutaway. https://www.ulalaunch.com/docs/default-source/rockets/atlasv-cutaway.pdf